optimization0906
최적화 수업 0906
0906 수업요약


Convex Sets & Convex functions

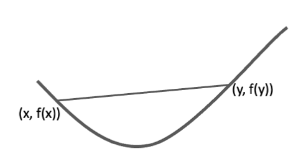
Relation between a convex set and a convex function
함수 f 의 epigraph가 convex set일때, 함수 f 는 convex function이다.
epigraph 란?
epi : above, 즉 그래프 위쪽 영역

역도 성립, 함수 f가 convex function일때 epi (f)는 항상 convex set.

- Optimization 문제를 convex function으로 변환하면 쉽게 풀 수 있다. 하지만, 가끔씩 내가 풀려는 문제가 convex function로 정의된 것인지 판단하기 어려울 때가 있다. 이럴 때는 함수의 epigraph가 convex set인지를 확인해서 convex function임을 판별할 수가 있다.
examples of convex functions
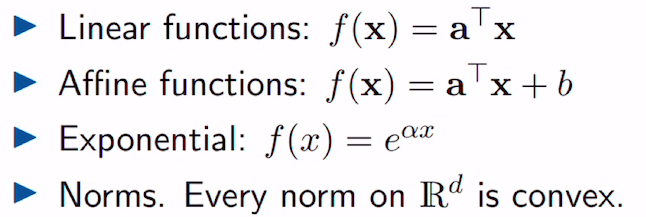
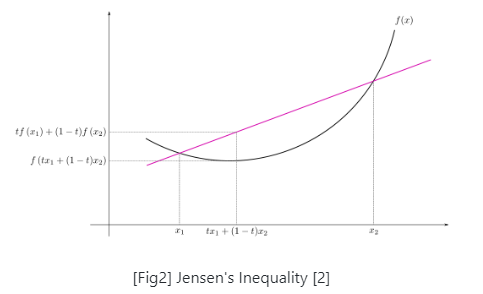
Jensen’s inequality

example ) 함수 f 가 convex 이면 다음이 성립.
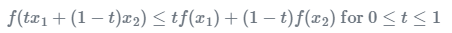
Convex functions are continuous
만약
1) f: convex function
2) dom(f) is open
-> f is continuous
First-order Characterization of convexity
graph f is abobe all its tangent hyperplanes
Second-order Characterization of convexity


Operations that preserve convexity
여기서는 convex function 의 convexity를 유지하는 연산에 대해 살펴본다. Convex fnuction의 Convexity를 유지하는 연산에는 다음과 같은 것들이 있다.

lemma (i)는 nonnegative linear combination으로 convex f함수들에 음수가 아닌 람다에 대한 선형 조합들은 convex이다.
lemma(ii)는 m차원->d차원 으로 매핑하는 함수 g(x) = Ax+b 가 있을때 f(Ax+b) 는 convex이다.
Local minima are Global minima

로컬 미니멈 정의와, 컨백스 함수에서는 로컬 미니멈이 글로벌 미니멈 에 대한 증명.
Critical Points are Global minima

함수가 open domain에 미분가능 할 때
critical points(임계점) 일때 -> Global minimum 이다.
이는 First-order characterization of convexity 이용해서 증명가능.
1일차 수업 끝.

댓글남기기