Optimization0913

최적화 수업 0913

---

Strictly Convex function

strictly convex function 정의, 글로벌 미니멈 한개임.

Constrained minimization

함수 f 가 convex 이고 , dom(f)[convex set] 일때 minimizer x 의 정의.

lemma는 밑에 그림보면 수식 이해감.

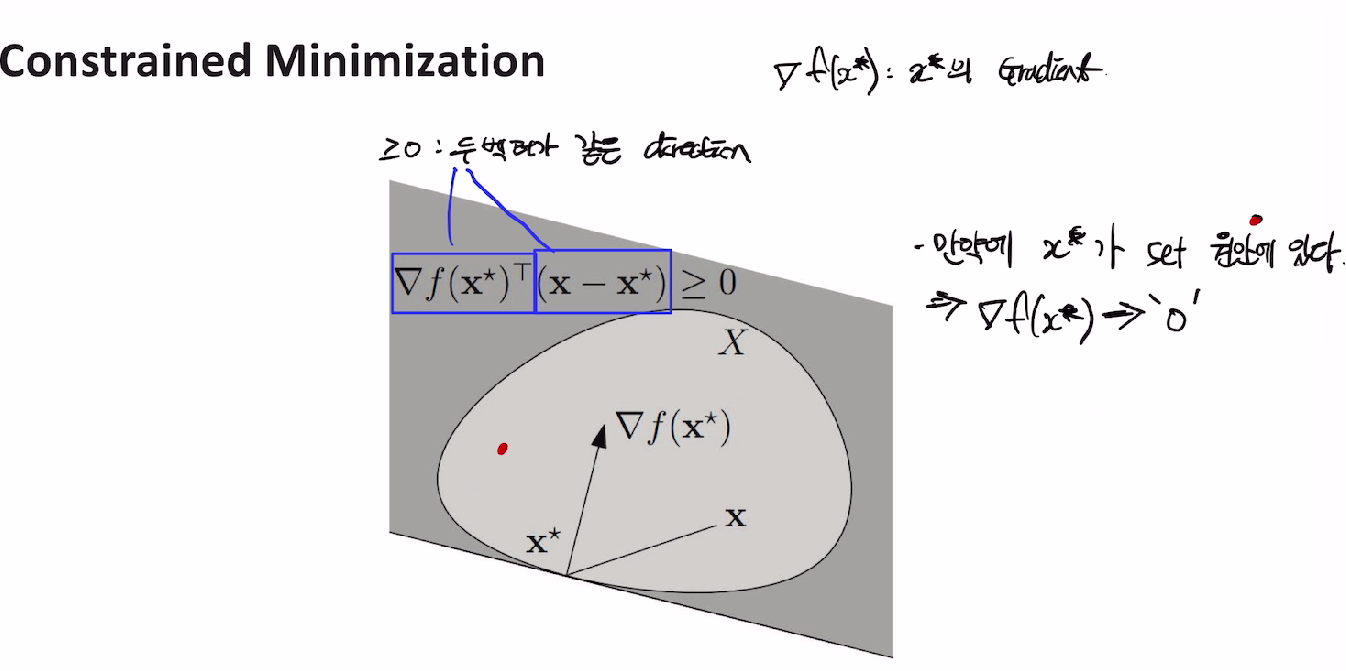
Existence of minimizer

그럼 global minimum 존재 어떻게 알아?

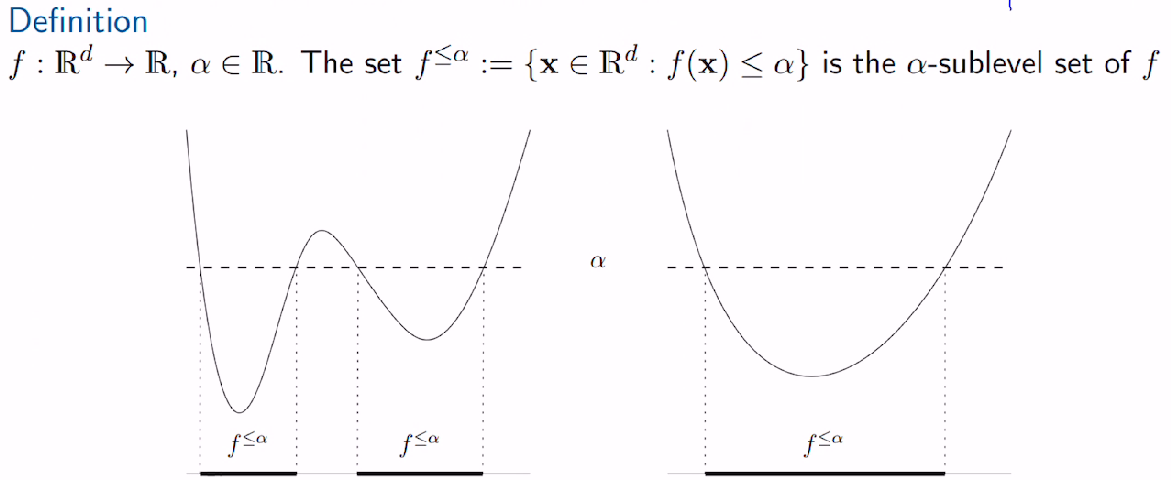
The Weierstrass Theorem

---

lec(2) 강의노트.

The Algorithm

미니멈x* 에 가까워 지고 싶고, 옵티멈f(x*)를 알고 싶어?

목표는 f(x)-f(x*) =입실론 이다.

iterative algorithm 사용해서 찾아보자.

하지만 장단점 존재

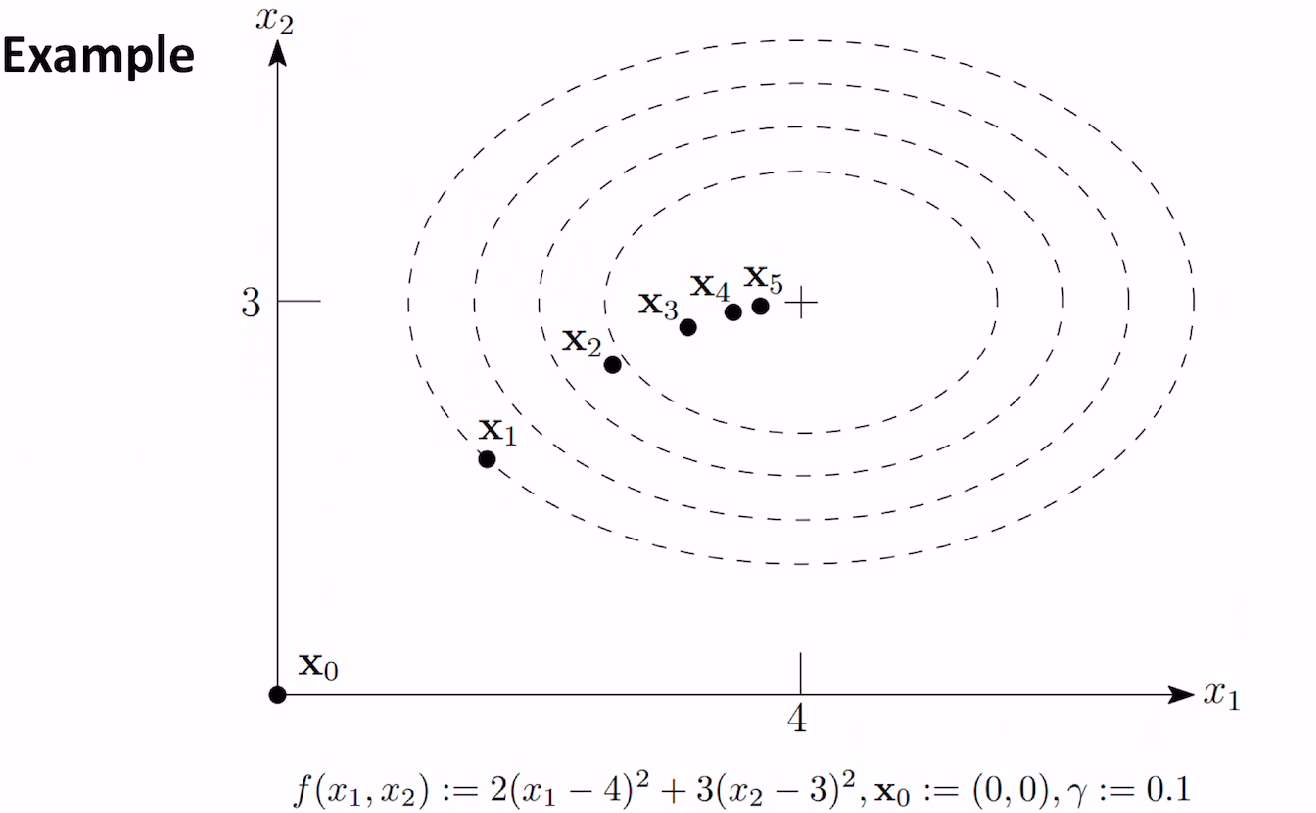
quadratice 예를 들어보자.

Quadratice example

line search는 스텝사이즈 r을 정하는 방법.

x0 과 step size 정해주면 다음과 같은 식으로 나타낼 수 있다.

Vanilla analysis

vanilla analysis로 인해서

평균 오차에 대한 upper bound가 나옴.

이는 gradient, initial point, step-size 에 의해서 결정이 된다.

Lipschitz convex functions

(STEP SIZE를 고르는 방법은 크게 fixed step size를 취하는 방법과, 매번 optimal한 step size를 고르는(update 하는) line search 방법이 있다.)

먼저 fixed step size에 대해 살펴보자.

앞선 평균 오차 때문만 아니라 step size를 잘 잡는것은 매우 중요하다. 너무 큰 step size 잡으면 algorithm이 diverge 하고, 작게 잡으면 느리기 때문이다. 그래서 step size를 잘 잡는게 중요한데, 다행이 어떤 적절한 step size에 대해 algorithm이 strictly convex function f의 global unique optimum으로 수렴한다는 것을 증명할 수 있다.

적절한 step size에 대해 설명을 하려면 먼저 L-Lipschitz function이라는 것을 정의해야하는데, 이는 다음과 같이 정의된다.

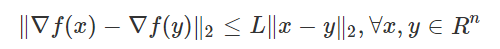
L은 함수가 얼마나 빨리변하는지를 나타낸다.

f가 L-Lipschitz function이고 어떤 optimum이 존재한다면 r(fixed step size) ≤2/L 을 취했을 때 gradient descent algorithm이 stationary point로 수렴하게 된다는 것을 증명할 수 있다.

평균값 정리 이용해서 표현가능.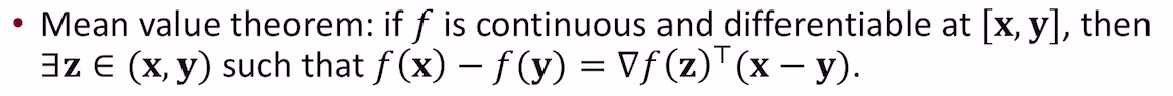

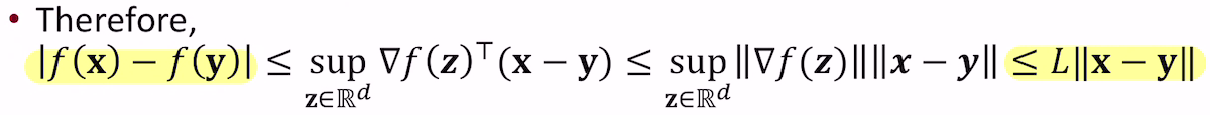
앞서 말한 적절한 step size를 구하기 위한 Theorem 이다.

함수 f가 convex이고 global minimum x* 에서 미분가능 할 때, x0(initial)-x*(minimizer)차이가 R 이하, 그래디언트가 B이하 일 때

step size를 R/B(sqrt(T)) 로 잡으면 , average error(normalization한)는 upper bound 를 가진다.

증명은 앞선 Vanilla Analysis 에서 추가된 가정들을 넣고, upper bound를 최소화 하기 위해 step size에 대해 미분을 한다.

그리고 upper bound 의 최솟값을(step size에 대한) 넣어주고 양 변을 T로 나누면 된다.

하지만

R(x0(initial)-x*(minimizer)차이 upper bound) , B(그래디언트놈 upper bound) 알 수가 없다.

Smooth functions

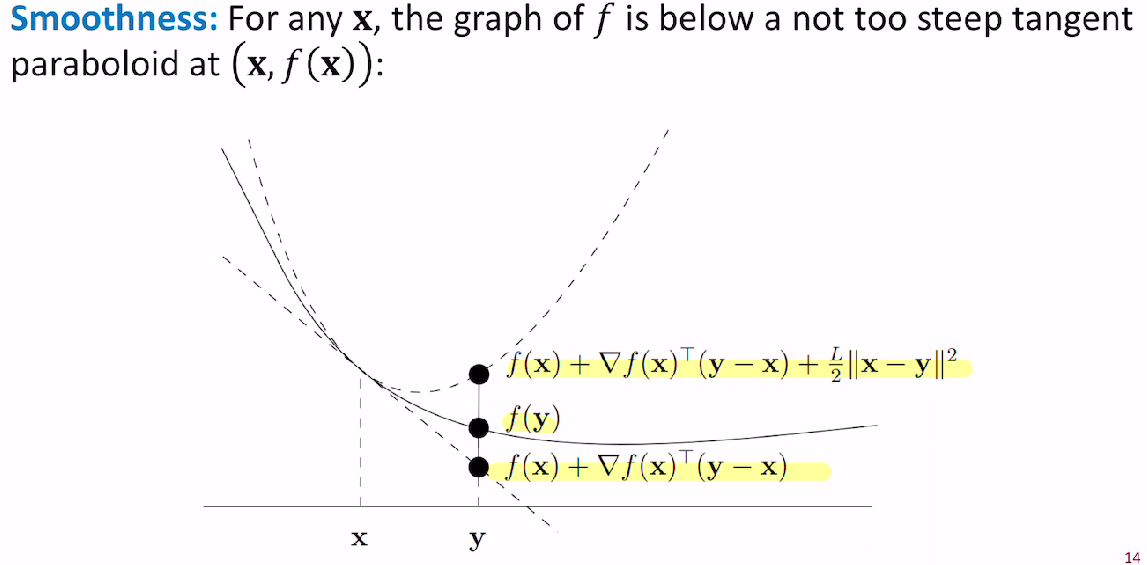
sufficient decrease

Smooth Convex functions

step size를 L로 잡는다면? (현재 함수값 - 최소 함수값) upper bound가 나오네.

---

토->일 멈춤.